Kā rodas bezskaidrā nauda? Stāsts par kredītu, naudu un bankām

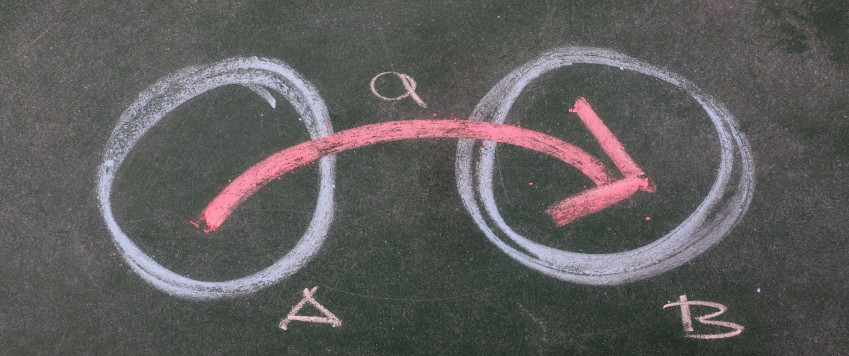
Vai, vērojot saulrietu vai saullēktu, kādreiz esat aizdomājušies, kādēļ ir tik grūti iztēloties jeb izveidot prātā modeli, kāds ir šo dabas parādību veidošanās mehānisms? Pirmkārt, mēs nevaram paskatīties uz sistēmu kopumā no malas, jo redzam apkārtējo pasauli tikai no sava skatpunkta. Tāpat šo dabas parādību apzīmēšanai izmantotie vārdi paši par sevi var radīt paradoksa sajūtu, kad pirmo reizi uzzinām, ka saulrietā un saullēktā tā nav Saule, kas lec vai riet. Kad iztēlojamies, kā ap mums ir iekārtota pasaule un darbojas mūsu radītas sistēmas, arī mūsu izmantotā valoda un vārdi zināmā mērā ietekmē, kā tiecamies izprast notiekošo.

Ekonomists Džons K. Galbraits (John Kenneth Galbraith) ir teicis, ka veids, kā bankas rada naudu, ir tik vienkāršs, ka prāts atsakās to pieņemt [2]. Varētu būt vairāki iemesli, kādēļ cilvēku prātam ir grūti pieņemt, kā mūsdienu digitālajā pasaulē funkcionē banku un daļējo rezervju naudas sistēma [3]. Kad spriežam par banku sistēmas darbību, mēs joprojām tiecamies iztēloties vienas atsevišķas bankas darbības modeli, saskaņā ar kuru banka no noguldītājiem iegūst līdzekļus, kurus izsniegt aizdevumos kredītņēmējiem.

Priekšstats par bankām kā starpnieku starp noguldītāju un aizdevuma saņēmēju zaudē jēgu, tiklīdz runājam par bankām kā visu sistēmu kopumā. Atšķirtībā no atsevišķas, jo īpaši nelielas, kredītiestādes darbības modeļa, kuru redzam 1. attēlā, bankas, ar to domājot visas bankas kopā, aizdevumos neizsniedz noguldītāju naudu, bet par depozītiem dēvēto bezskaidro naudu, ko pašas rada no jauna. Galbraita pieminētais fenomens, ka ar prātu nespējam tādu ideju pieņemt, nav pārsteigums, ja lietojam vārdus, kas vēsturiski ienākuši valodā, runājot par bankām. Teiktais, ka jauni naudas noguldījumi nerodas, noguldot naudu, izraisa neticības vai jau pieminēto paradoksa sajūtu. Galu galā vārds noguldījumi, kas iesakņojies, lai apzīmētu banku bezskaidro naudu, ir radniecīgs vārdam noguldīšana, ko joprojām iztēlojamies kā taustāmas formas naudas noglabāšanu.

Skaidrojums, ka naudas noguldījumi visbiežāk rodas kā ar jaunu kredītu saistīts uzskaites ieraksts banku bilancē šķiet pretrunā tam, kā iztēlojamies noguldījumu veidošanos. Raksta turpinājumā mēģināšu sniegt citādu uzskatāmāku modeli par naudas rašanos banku sistēmā, izmantojot piemēru, kā mēs paši ikdienā dažkārt izmantojam uzskaites sistēmu, kas ir līdzīga bezskaidrai naudai kredītiestāžu bilancē.

Savstarpējo norēķinu uzskaites grāmatas modelis

Naudas izmantošana padara savstarpējos norēķinus ērtus un raitus, tomēr skaidrās naudas formai piemīt savi ierobežojumi. Ir nepieciešams turēt pietiekoši lielu un dažādu nominālu naudaszīmju krājumu, lai praktiski panāktu naudas dalāmību. Tāpat tiek patērēts laiks maksājuma veikšanai, skaitot un pārskaitot naudu. Biežu secīgu maksājumu gadījumā šis process kļūst manāmi laikietilpīgs.

Visuzskatāmākais pielietojums, kurš ļauj demonstrēt bezskaidras naudas rašanās motivāciju un vienlaikus arī mehānismu, ir punktu skaitīšana kāršu spēlēs. Spēlēs, kur zaudētājiem pēc katras pabeigtas partijas jāsamaksā uzvarētājiem noteikta naudas summa, nav ērti veikt maksājumus skaidrā naudā. Punktu skaitīšana ļauj atrisināt skaidrās naudas dalāmības problēmu, kad savstarpējie norēķini pēc katras partijas var nebūt iespējami. t.i., norēķinus, izmantojot skaidro naudu, dalībniekiem par to vienojoties, var aizstāt ar ērtāku risinājumu, ieviešot naudas vienībās izteiktus spēles punktus jeb kredītus.

Atšķirībā no ierastās prakses, kad punktus pēc katras pabeigtas partijas pieraksta, raugoties no katra spēlētāja bilances, cik naudas katrs spēlētājs ir ieguvis vai zaudējis, paraudzīsimies uz procesu kā “Spēles bankas” dibināšanu un darbību, un aplūkosim šī nodibinājuma bilanci.

Tātad, lai apliecinātu gatavību pildīt savas saistības, spēles biedri – draugi – nodibina “Spēles banku”, katrs iemaksājot bankas kapitālā noteiktu naudas summu un kļūstot par ”akcionāriem”. Šajā brīdī “Spēles bankas” bilancē saistību pusē ir saistības pret akcionāriem jeb kapitāls, bet aktīvu pusē – iemaksātā skaidrā nauda jeb skaidrās naudas rezerves. Turpmāk uz laiku  spēlētāji vienojas neizmantot skaidro naudu, bet savstarpējos norēķinus veikt tikai  naudas vienībās izteiktos punktos.

Noslēdzoties pirmajai spēles partijai, uzvarētājiem būtu jāsaņem punkti, bet nevienam no dalībniekiem to vēl nemaz nav. Tā kā zaudētājam maksājumu veikšanai nepieciešami punkti, viņi tos aizņemas no “Spēles bankas”, kura tos izsniedz kā kredītu jeb aizdevumu – prasības atmaksāt bankai skaidro naudu, t.i., “Spēles banka” izsniedz punktu kredītu, kuru tālāk pārskaita uzvarētājiem. Savukārt uzvarētājiem izveidojas šo punktu noguldījums “Spēles bankā”.

Raugoties uz “Spēles bankas” bilanci, tās aktīvu pusē pievienojies kredīts (negatīva punktu bilance kādiem no spēlētājiem jeb parādsaistības pret banku) – prasības pret spēlētajiem, savukārt bilances saistību pusē ir saistības (pozitīva punktu bilance kādiem no spēlētājiem jeb prasības pret banku) Pēc pirmās spēles banka un kredītņēmēji ir apmainījušies ar saistībām – banka nodrošina kredītņēmēja (pirmās spēles zaudētāja) nepieciešamību pēc spēles punktiem, lai tos pārskaitītu izspēles uzvarētājiem. Šos spēles punktus uzskaita “Spēles bankas” bilances saistību pusē, t.i., nauda rodas, kreditējot aizdevuma saņēmēja kontu. Savukārt aktīvu pusē līdzās rezervēm banka iegūst prasības pret “klientu”.

Pieņemsim, ka draugi vēlas šo uzskaites grāmatu izmantot arī citiem savstarpējiem norēķiniem, piemēram, par izdevumiem, kas iepriekš radušies, organizējot spēļu vakara pasākumu., t.i., pēc abpusējas vienošanās pieņemt spēles punktus darījumos, kas ir jau ārpus punktu naudas plūsmām spēlē. Ja kādam dalībniekam nepietiek punktu attiecīgo maksājumu veikšanai, ir vienkāršs risinājums – “Spēles banka” izsniedz spēles punktu kredītu, ja uzskata, ka kredītņēmējs nokārtos papildu saistības. Ja dalībnieku pieprasījums pēc kredīta pārsniedz “Spēles bankas” kapitālā iemaksātās skaidrās naudas rezerves (turpmāk tekstā – rezerves) un dalībnieki neiemaksā kapitālā papildu skaidro naudu, tad spēles punktu vērtība naudas izteiksmē pārsniedz rezerves jeb rezerves tikai daļēji nosedz ar spēles punktu “noguldītāju” prasības pret “Spēles banku” izmaksāt skaidro naudu.

Tā kā banku sistēmai, kuru veido daudzas kredītiestādes, varam izveidot apkopoto bilanci, un uz to raudzīties kā vienu veselu kredītiestādi, esam izveidojuši daļējo rezervju sistēmas modeli.

Atkarībā no vienošanās norēķinus ar skaidro naudu var pabeigt spēļu vakara noslēgumā, vienlaikus veicot “Spēles bankas” likvidāciju – katram nokārtojot saistības pret banku un bankai izmaksājot attiecīgo skaidrās naudas summu atbilstoši uzkrātajiem spēles punktiem. Tomēr, ja spēļu vakari ir regulāri un, piemēram, nedēļas nogalēs seko cits citam, dalībnieki var vienoties saglabāt kredītsaistības un punktu noguldījumus bez noteikta beigu termiņa.

Aplūkotais modelis demonstrē efektivitāti, kāda piemīt nemateriālas formas naudai. Ja ir pieprasījums pēc punktiem (naudas pieprasījums), kurus var apmainīt pret precēm, papildu nepieciešamo naudu var radīt praktiski bez izmaksām; tai piemīt norēķinu un uzskaites vienkāršība; neatņemama sastāvdaļa ir centralizēts visu ar bankas naudu veikto darījumu vēstures pieraksts, t.i., bezskaidras naudas izmantošana rada mazākas izmaksas, kas saistītas ar pašu naudas izmantošanu. Tāpat redzams, ka aizdevumā netiek aizdota skaidrā nauda, bet tiesības no bankas pieprasīt skaidro naudu, ja tā ir nepieciešama. T.i., bezskaidrās naudas rašanos un jaunu līdzekļu ievietojumu tautsaimniecībā nosaka tirgus – ja ir pieprasījums pēc kredītiem un kredītiestādes ir gatavas to apmierināt, un puses var vienoties par likmi, tad lai top jauna nauda!

Nauda kā uz uzticēšanos balstīta sociāla vienošanās

Raugoties tikai uz pašu uzskaites mehānismu, kā rodas bezskaidra nauda, var šķist, ka mūsu modelī “spēles nauda” rodas “no zila gaisa”. Tomēr paliek nepamanīts, ka šāda efektīvāka norēķinu mehānisma darbību nodrošina ļoti būtisks nemateriāls faktors – uzticēšanās. It kā pats par sevi saprotamais fenomens, ka draugi iepriekš aplūkotajā piemērā vienojas skaidrās naudas vietā izmantot ērtāku savstarpējo norēķinu shēmu un var to izmantot arī ar spēli nesaistītiem savstarpējiem norēķiniem, ir iespējams, jo starp viņiem pastāv uzticēšanās, ka katrs spēs un varēs nokārtot savas saistības.

Šis modelis parāda, ka nauda izveidojas kā sociāla vienošanās, jo modelī spēles punktu vērtība rodas dēļ izmantošanas iespējām, kas ir atkarīgas no tā, vai sabiedrība piekrīt to izmantot un pieņem preču un pakalpojumu maiņas attiecībās. T.i., uzskaites ieraksti, kuriem pašiem par sevi nav nekādas vērtības, tiek izmantoti reālas vērtības maiņai. Naudas vērtības pamats ir uzticēšanās un vienošanās, ka pārējie tautsaimniecības dalībnieki to pieņems, rezultātā visi kopā gūstot labumu, ko sniedz efektīvāks preču un pakalpojumu maiņu nodrošinošs mehānisms.

Tomēr tikai uz savstarpēju uzticēšanos balstīta modeļa mērogam ir robežas. Tas vēl var darboties kādā kooperatīvā krājaizdevu sabiedrībā, piemēram, Šveices vai Vācijas ciematā, kurā no seniem laikiem mītošu dzimtu pārstāvji pazīst viens otru daudzās paaudzēs un savstarpēji aizdevumi iespējami uz savstarpējas uzticēšanās un kopīgu zināšanu pamata vienam par otru.

Banku loma ir padarīt mijiedarbību iespējamu visas tautsaimniecības mērogā, t.i., starp tautsaimniecības dalībniekiem, kuriem nav personiskā pamata citiem uzticēties un nav zināšanu par citu spēju pildīt kredītsaistības. Vienlaikus bankas nodrošina, ka apstākļos, kad tautsaimniecībā ir nepieciešamība pēc papildus līdzekļiem, noteikto regulējošo normatīvu ietvaros un izvērtējot naudas saņēmēja spēju naudu atmaksāt, nauda tiek radīta, izsniedzot kredītu. Šāds uz tirgus principiem balstīts naudas sistēmas darbības modelis atrisina centrālās plānošanas informācijas problēmu – kam un kādā apmērā piešķirt līdzekļus, lai rezultātā ieguvēji būtu gan attiecīgais tautsaimniecības dalībnieks, gan visa tautsaimniecība kopumā.

Cena, kura ir “jāmaksā” par sistēmas priekšrocībām, ir daļējo rezervju sistēmas pašos pamatos ieliktā nestabilitāte gadījumā, ja tiek zaudēta uzticēšanās savstarpējai spējai pildīt saistības. Uzticēšanās ir neredzams resurss, kura klātesamība banku sistēmas sekmīgai darbībai ir jānodrošina ik dienu. Tādēļ naudas sistēmas darbība nav iespējama bez kredītiestāžu uzraudzības, kā arī makroekonomiskās analīzes, kā banku darbība ietekmēs emitētās naudas pirktspēju jeb vispārējo cenu līmeni tautsaimniecībā.

Noslēdzot šo rakstu, kura mērķis ir ilustrēt bezskaidras naudas rašanās principus, jāpiebilst, ka tas ir kontrolējams mehānisms un banku bilances un attiecīgi naudas apjoma palielināšanos var ierobežot, izmantojot pašu banku bilances rādītājus. T.i., var ieviest skaitliskus kritērijus, piemēram, mazāko pieļaujamo rezervju-noguldījumu attiecību jeb minimālo rezervju normu [6] un bankas kapitāla attiecību pret bankas izsniegto kredītu apjomu, kas līdz ar daudziem citiem atsevišķu kredītiestāžu un banku sistēmas uzraudzības un monetārās politikas instrumentiem kalpo sistēmas stabilitātes nodrošināšanai.

Pēcvārda vietā: kur pazudis naudas multiplikators?

Rakstā aplūkotajā modelī, kā tautsaimniecībā rodas naudas piedāvājums, ne reizi netika izmantots naudas multiplikatora jēdziens. Pats skaidrojums, ka bankas “multiplicē naudu”, var padarīt naudas rašanās skaidrojumu grūtāk izprotamu. Kādēļ kredītiestāžu darbības raksturošanai tiek izmantota tieši šī aritmētiskā darbība, nevis, piemēram, saskaitīšana vai kāpināšana? Tiesa, naudas reizinātājs ir noderīgs, aplūkojot naudas apriti pirms digitālo tehnoloģiju ienākšanas banku darbībā un banku piedāvātajos pakalpojumos.

Kamēr naudu var iedalīt divās atšķirīgās kategorijās – (skaidrā) nauda un (skaidrās) naudas noguldījums bankā, kuru banka savukārt izsniedz skaidrā naudā kā aizdevumu, naudas multiplikators rāda, cik reizes vidēji viena apgrozībā esoša skaidrās naudas vienība ir tikusi noguldīta bankās un pēc tam atgriezusies atpakaļ tautsaimniecībā kā naudas aizdevums. Naudas reizinātājs skaitliski parāda šo skaidrās naudas aprites ciklu skaitu. Aplūkojot naudas sistēmu, kurā skaidrā nauda aizvien vairāk ieņem nišas lomu, bet galvenā norēķinu naudas forma tautsaimniecības apritē ir banku nauda, naudas multiplikatoru varētu interpretēt vairs tikai kā ekonomisku multiplikatoru – cik reizes palielinātos kopējais naudas apjoms tautsaimniecībā, ja centrālā banka palielinātu savu naudas piedāvājumu kredītiestādēm.

Mūsdienās attīstītajās valstīs, kuras monetārās politikas īstenošanai atteikušās no tiešas naudas apjoma regulēšanas, bet tā vietā raugās uz procentu likmju piemērotību inflācijas mērķa sasniegšanai, naudas reizinātāju vairs nevar uzskatīt arī par ekonomikas multiplikatoru. T.i., tas vairs nav banku darbību raksturojošs pastāvīgs skaitlisks lielums, bet naudas reizinātāja vērtība mainās līdz ar centrālas bankas naudas piedāvājumu.

Literatūra

1. Kā rodas nauda mūsdienu monetārajā sistēmā? Centrālās bankas loma un iespējas
2. Likviditāte un tās vadīšana Eiropas monetārajā savienībā
3. Valdības finanšu loma naudas emisijā – fiskālās politikas monetārā ietekme

[1] Language shapes the way we think, and determines what we can think about. (Benjamin Lee Whorf)

[2] The process by which banks create money is so simple that the mind is repelled. Where something so important is involved, a deeper mystery seems only decent. (John Kenneth Galbraith)

[3] Kredītiestāžu darbības regulējums, saskaņā ar kuru tikai noteiktai daļai no kredītiestādes depozītsaistībām un citām līdzvērtīgām saistībām jābūt segtām ar centrālās bankas emitēto naudu jeb rezervēm.

[4] Life is a game. Money is how we keep score. (Ted Turner)

[5] “Trust is like the air we breathe – when it’s present, nobody really notices; when it’s absent, everybody notices.” (Warren Buffett)

[6] Regulējums, saskaņā ar kuru kredītiestādes rezervju un noguldītāju depozītu attiecība vidēji nedrīkst būt mazāka par noteiktu vērtību – minimālo rezervju normu.